Connected Components Matrix

A counter is initialized to count the number of objects.

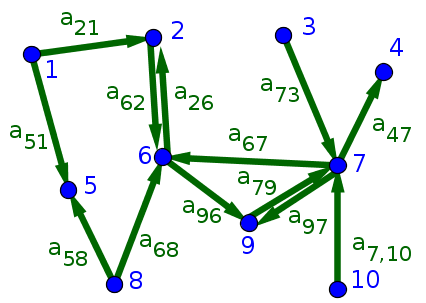
Connected components matrix. A strongly connected component scc of a directed graph is a maximal strongly connected subgraph. Tarjan s algorithm to find strongly connected components finding connected components for an undirected graph is an easier task. As discussed in section 3 the ranking algorithm requires a suitable connectivity matrix to be identified. The trace of the laplacian matrix l is equal to textstyle 2m where.

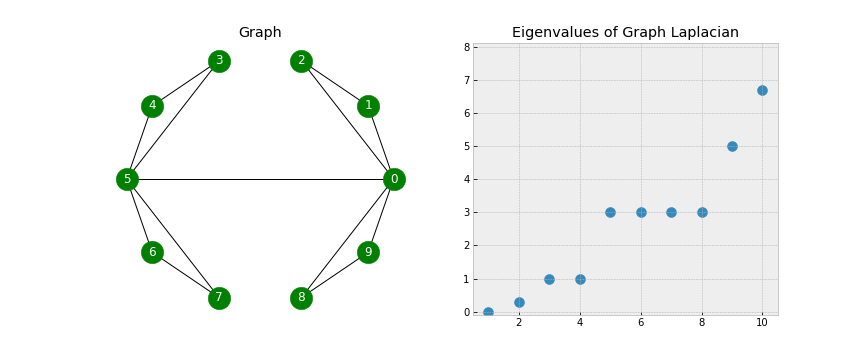
Implementation of connected components in three dimensions using a 26 18 or 6 connected neighborhood in 3d or 4 and 8 connected in 2d. First we prove that a graph has k connected components if and only if the algebraic multiplicity of eigenvalue 0 for the graph s laplacian matrix is k. We then prove cheeger s inequality for d regular graphs which bounds the number of edges between the two subgraphs of g that are the least connected to one another using the second smallest. Connected components of an image or matrix image components is a fortran77 library which seeks to count and label the connected nonzero nonblack components in an image or integer vector matrix or 3d block.

We simple need to do either bfs or dfs starting from every unvisited vertex and we get all strongly connected components. Connected component matrix is initialized to size of image matrix. A mark is initialized and incremented for every detected object in the image. Below are steps based on dfs.

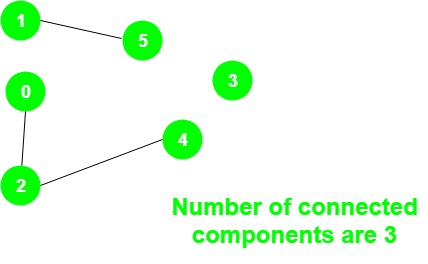
For a graph with multiple connected components l is a block diagonal matrix where each block is the respective laplacian matrix for each component possibly after reordering the vertices i e. L is permutation similar to a block diagonal matrix. A row major scan is started for the entire image. For example there are 3 sccs in the following graph.