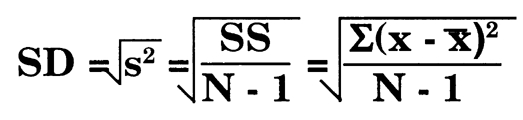Cv Mat Variance

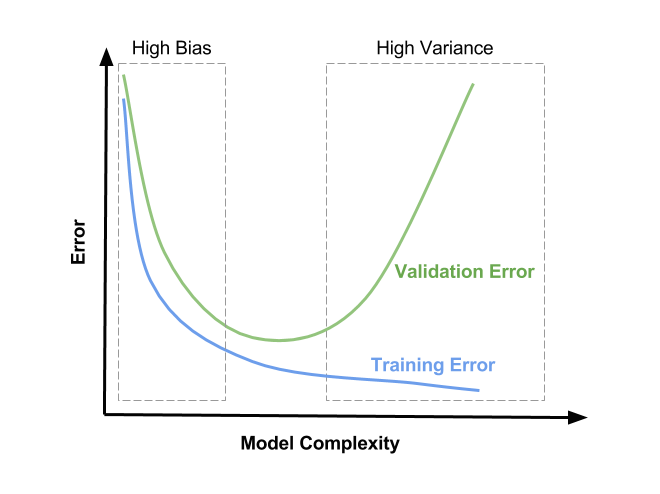
An example using pca for dimensionality reduction while maintaining an amount of variance.

Cv mat variance. Cv getcv x compute the coefficient of variation c v of the input vector x. Input vector output cv. The function ignores nans. If a is a matrix whose columns are random variables and whose rows are observations v is a row vector containing the variances corresponding to each column.

Github is home to over 50 million developers working together to host and review code manage projects and build software together. Cv vl where the covariance matrix can be represented as c vlv 1 which can be also obtained by singular value decomposition. If a is a multidimensional array then var a treats the values along the first array dimension whose size does not equal 1 as vectors. In probability theory and statistics a covariance matrix also known as auto covariance matrix dispersion matrix variance matrix or variance covariance matrix is a square matrix giving the covariance between each pair of elements of a given random vector in the matrix diagonal there are variances i e the covariance of each element with itself.

If a is a vector of observations the variance is a scalar. Output nx1 matrix with computed variance. The eigenvectors are unit vectors representing the direction of the largest variance of the data while the eigenvalues represent the magnitude of this variance in the corresponding directions. Computes the mean and variance of a given matrix along its rows.

In our example the variance was 200 therefore standard deviation is 14 14. Output nx1 matrix with computed mean. Vice versa variance is standard deviation squared. It computes in the same way as woud do reduce but with variance function.

Coefficient of variation a scalar. To calculate standard deviation from variance only take the square root. Dismiss join github today.